Then we take the transpose of this matrix and multiply it against the first in an ATA fashion.
giving us the following result
We then find the eigenvalues of this matrix by subtracting λIn and then solve the characteristic equation.
The characteristic equation is found by taking the determinant of the adjusted matrix.
(40-λ)(85-λ)-(-30)(-30) = 0
3400 -125 λ + λ2 - 900 = 0
λ2 -125 λ + 2500 = 0
(λ-25)(λ-100)=0
λ = 25,100
σ1=10, σ2=5
giving us an S matrix ofThese values will also be used in creating our U matrix. But in order to find our U matrix we must first find our V matrix so we need to orthogonalize the eigenvectors from our ATA matrix. Our first step will be to substitute in our eigenvectors in the same order we have our sigma values.
So solving for the kernel by setting this equal to 0 gives us the vector
So after solving for the kernel we will get the vector
Now we have to normalize these two vectors so we take their magnitude, and divide the vectors by this amount.
((12) + (22))1/2
(5)1/2
To form the U matrix we use the following method to compose the u vectors.
un=Avn/σ
u1=Av1/σ
u2=Av2/σ
Now we get the combined U matrix of
This gives us all the parts we need to find the svd decomposition, the only difference is that our V matrix is actual V transpose in the equation so we have the following matrixes
And the equation to regain our original matrix is M = USVT. You can check my multiplying these out to confirm that they give you the original matrix. Thus we have completed our singular value decomposition of our matrix!



















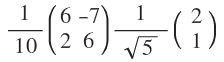




No comments:
Post a Comment